How To Divide Fractions?

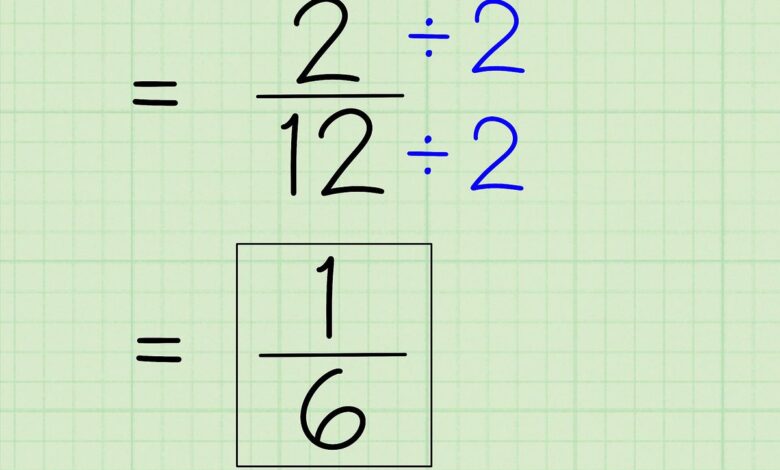
Just like many other generic operations infractions such as adding fractions, subtracting them, multiplying them, there is the operation of dividing fractions. Division of an object means sharing it equally; we are already familiar with concepts such as division of whole numbers, decimal numbers, etc. Now we are going to learn about the division of fractions. A fraction as we already know has two parts. The numerator and denominator. The upper part is called the numerator while the part at the bottom is known as the denominator. Dividing fractions is nothing but multiplying them. For division, we multiply the first fraction by the inverse of the second. That gives us the result of division.

Methodology of division:

For the concept of division of fraction, we can get a clear understanding with the help of an example:

                       (4/3)/(3/5)= 4/3*5/3= 20/6

In the example given above, we can see that 4/3 is to be divided by 3/5. So what we do is we multiply 4/3 by the reciprocal of 3/5 which is 5/3. So now the question becomes 4/3*5/3 which is straight multiplication so the answer is 20/6.

So evidently the thumb rule is (a/b)/(c/d)= a/b*d/c= ad/bc. Solely for the purpose of division.

Division of fractions with decimals or by decimals:

For the division of fractions with decimals or by decimals, we just have to write the given number with decimal in the form of a fraction. To get a clear understanding let’s start with an example:

                      (7/5)/0.5= (7/5)/(5/10)=7/5*10/5=70/25

In the above example, we see that we are dividing a fraction by a decimal number. So we convert that decimal number into a fraction first. To do so in 0.5 we see that after decimal there is only one digit, so while we remove the decimal, we place one 10 below it. Thus 0.5 becomes 5/10. Then it is just the normal division of fractions which we have already learned. That is reciprocating the below fraction to multiply it with the upper fraction to obtain the result.

Division of mixed fractions:

The methodology of the division of mixed fractions is also fairly simple in nature. To kick things off we convert the given mixed fractions into improper fractions. Then we perform the simple division of fractions. To convert mixed fractions into an improper fractions we multiply the denominator by the whole number part and add the numerator to it. Like suppose the mixed fraction which is given is 8  7/5 (read as 8 whole 7 by 5). 8 is the whole number part here and 7 and 5 are the denominator and numerator respectively. To convert it into an improper fraction we multiply 5 by 8 and add 7 to it. So the improper fraction becomes 47/5.

Let us try understanding by examples for better understanding:

(7  9/2)/(9  8/2)= (23/2)/(26/2)= 23/2*2/26= 23/26.

Learning division of fractions:

These concepts basically are taught to elementary grade students. But sometimes the intricacies of the concept of division of fractions and some of the aspects can be quite intimidating and bewildering for beginners. But there isn’t much to worry about as  Cuemath has got the backs of those students in need. With the interactive and engaging interface of the website of Cuemath, children tend to focus more easily, and the process of learning becomes more fun for them and they tend to remember concepts for a longer time more efficiently. This eliminates the scope of children getting bored as the usual boring and tiresome concept learning methodology is no longer in use. Efficient learning is the only thing Cuemath believes in.

Conclusion:

Upon retrospecting on the facts and details mentioned above we arrive at a respectable conclusion that mentioned concept with being important to the subject mathematics is also equally important to the concept building aspect as it is recognized as a concept-building block. The many important features listed are just a sample; the whole picture of its sheer importance is difficult to put in words.